A story that contains physics and comedy is never an easy recipe. The mixture is never easy to get right, but this time, the outcome is purely delicious. Let's see what it takes to throw a big sack (27kg) over a very tall wall (10 meters).
SUPPOSE SOMEONE BUILDS a wall. A great and tall wall that is both impenetrable and beautiful. Who knows—maybe it's even solar powered. This wall stands 10 meters tall and goes on and on and on.
Two question we will answer:
1) How much force must be applied to get this bag over that wall?
2) And what happens if the bag bonks someone on the other side?
Let's get started!
I find that the best way to start just about any physics problem is to diagram it. Visualizing the problem helps determine just what you need to solve for and what you already know. Plus, I like making diagrams.
1) How much force must be applied to get this bag over that wall?
2) And what happens if the bag bonks someone on the other side?
Let's get started!
I find that the best way to start just about any physics problem is to diagram it. Visualizing the problem helps determine just what you need to solve for and what you already know. Plus, I like making diagrams.
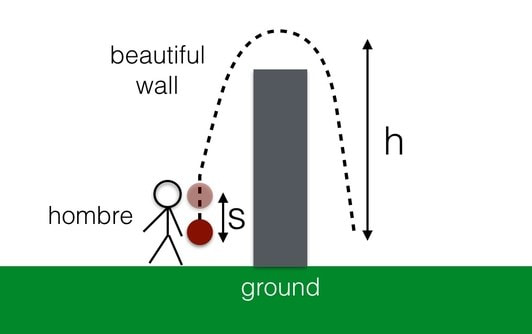
Now suppose someone wants to toss a bag of stuff over that wall. A big bag with a mass of, oh, 60 pounds. (I will say 27 kilograms, because kilograms are better.)
Yes, I know the diagram is not to scale. Don't worry about that. The key thing to consider is that the guy (or hombre—good or bad, you decide) must push this bag of stuff some distance s to get it up to speed. The sack then moves up to a height h so that it goes over that tall, glorious wall. Right here we should be able to see a path to the solution. We can solve this problem using the work-energy principle because we don't care about time, only distance. This principle says that the work done on a system is equal to the change in energy of that system.
Yes, I know the diagram is not to scale. Don't worry about that. The key thing to consider is that the guy (or hombre—good or bad, you decide) must push this bag of stuff some distance s to get it up to speed. The sack then moves up to a height h so that it goes over that tall, glorious wall. Right here we should be able to see a path to the solution. We can solve this problem using the work-energy principle because we don't care about time, only distance. This principle says that the work done on a system is equal to the change in energy of that system.
If I choose a system consisting of the sack and the Earth, we will see two types of energy in this system: kinetic energy and gravitational potential energy.
Here (g) represents the gravitational field with a value of 9.8 N/kg.
But what performs the work on this system? The man (or hombre), of course.
As the fellow pushes on (throws) the sack of stuff, he applies a force (F) over some distance (s). The angle between this force and displacement would be zero degrees such that the cosine would be 1. And so the total work is:
Now for the change in energy. If I consider the sack at the moment just before it's thrown the starting point, it starts with a kinetic energy of zero joules.
For the second point, I will use the highest point in the path at the sack clears the great and awesome wall. Here, too, the sack has a kinetic energy of zero joules. Therefore, the change in kinetic energy is zero joules.
For the gravitational potential energy, let's make the starting point y = 0 meters such that the initial potential is zero joules. At the highest point, this gives the sack a potential energy of mgh.
Making this work equal to the change in energy, I can solve for the required launching force (F):
For the second point, I will use the highest point in the path at the sack clears the great and awesome wall. Here, too, the sack has a kinetic energy of zero joules. Therefore, the change in kinetic energy is zero joules.
For the gravitational potential energy, let's make the starting point y = 0 meters such that the initial potential is zero joules. At the highest point, this gives the sack a potential energy of mgh.
Making this work equal to the change in energy, I can solve for the required launching force (F):
Now we plug and chug.
Using a sack mass of 27 kg (m) and a beautiful bodacious wall height of 10 meters (h), I just need a value for the distance (s) I am actually applying force to launch the sack. Let's be generous and give (s) a value of 1 meter—using both arms and legs to increase the distance of the launch zone.
This would require an average throwing force of 2,646 newtons, or almost 600 pounds.
That makes this one tough sack-throwing hombre, someone not to be messed with!
But wait! But what if that hombre hurls that sack over that mighty wall and bonks someone on the head? How do we find out what happens?
Well, the physics is exactly the same, but backward. If you caught this sack on the other side with a catching distance (s) of 1 meter, you would need an average force of 2,646 Newtons. If it hit you in the head, it might stop over a much shorter distance of about 0.25 meters (s).
In this case, there would be an impact force of 10,584 newtons. BAM! That would hurt.
Hopefully someone gives this massive magnificent wall some windows so you can see the sacks being tossed over.
Many thanks to Rhett Allain from Southeastern Louisiana University and Wired Magazine for this hilarious and insightful lesson on what it takes to throw a big sack of whatever over a wall. This article can be read in it's entirety at : Wired Magazine - Trump Wall.

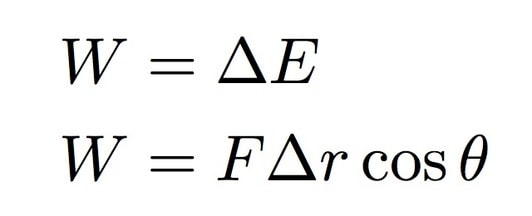
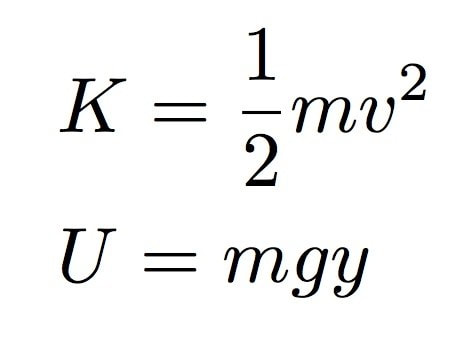
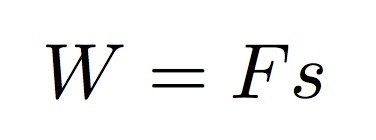
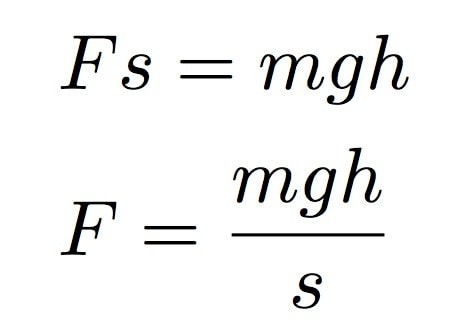
 RSS Feed
RSS Feed